However we also know binomial is an approximation of Poisson when the probability of an event is small. Poisson Distribution The second most frequently used discrete distribution after binomial distribution.
The key to using words that make you sound smarter is understanding how to use these terms properly and when to add them to.

. The sample space often denoted by is the set of all possible outcomes of a random phenomenon being observed. Linear Regression with Rare Events Linear Regression with Rare Events Rare event. A case study b.
Pr A 0. We must first introduce some notation which is necessary for the binomial. What is the benefit of using one rather than the other.
To describe the behavior of animals in their native habitats researchers are most likely to make use of naturalistic observation. Shape is similar to BinomialPoisson distribution. A probability distribution is a mathematical description of the probabilities of events subsets of the sample space.
No rule of thumb but Any disease is considered a rare event. An explanation using an integrated set of principles that organizes observations and predicts behaviors or events. With the following assumptions.
Add Solution to Cart. A 80 b 857 c 9567 d 120. The distribution used to describe the behaviour of rare events is the Poisson Distribution.
Poisson Distribution is a distribution function used to describe the occurrence of rare events or to describe the sampling distribution of isolated counts. The Poisson distribution is a discrete probability distribution that describes the probability of the number of events discrete random variable from a random process in a fixed interval. Rare Events the Sample Decision and Conclusion Establishing the type of distribution sample size and known or unknown standard deviation can help you figure out how to go about a hypothesis test.
Below is a preview of the main elements you will use to describe each of these concepts. The number of events per unit time is the same throughout the entire time interval t. From Poissons postulates we know Poisson works for rare events.
Pr left A right. The solution discusses binomial distribution used to model the number of rare events. A 50 b 52 c 60 d 70.
The third distribution is kind of flat or uniform. Probability distributions come in many shapes with different characteristics as. Or in a distribution of transformed standard scores with a mean of 100 and a standard deviation of 15 it could be reported as a score of.
The second distribution is bimodal it has two modes roughly at 10 and 20 around which the observations are concentrated. The first distribution is unimodal it has one mode roughly at 10 around which the observations are concentrated. We say the event A is rare or unusual if.
However there are several other factors you should consider when working out a hypothesis test. It may be any set. Center shape spread and outliers.
Mutation acquisition is a rare event. Earthquakes in the past million years not so rare. It is usually associated with rare events.
Looking for a list of words that describe behavior. A set of real numbers a set of vectors a set of arbitrary non-numerical values etc. A probability distribution depicts the expected outcomes of possible values for a given data generating process.
For example at any particular time there is a certain probability that a particular cell within a large population of cells will acquire a mutation. Number of items in a batch of random size. However the best rare words are ones you can use in daily life.
Number of events in an interval of time or area when the events are occurring at a constant rate. Any event as frequent as a disease can be considered rare. The rare event of interest is an extreme deliberate act of violence destruction or socioeconomic disruption such as an attack of 911 scale or greater.
A testable prediction often implied by a theory. Which of the following is NOT one of the descriptive method psychologist use to observe and describe behavior. Design reliability tests where the failure rate is considered to be constant as a function of usage.
A test score located one and one-third standard deviations below the mean could be reported as a z score of -133. Discrete random variables take a countable number of integer values and cannot take decimal values. It is not a realistic goal to anticipate and prevent all rare events but it may be possible to make.
Our rule of thumb. Naturalistic observation c. You are given an event you compute its probability if it is less than 005 or whatever the pre-specified threshold for unusual events is then it is considered to be rare or unusual otherwise it is a usual event.
Earthquakes in the past ten years rare. This means that the likelihood of an event is proportional to the size of the area of opportunity and that the rate of occurrence for the rare events is constant throughout the area of opportunity Next given that the counts are Poisson the times between events will be modeled by an exponential distribution. Depends on time unit.
The Poisson Distribution is a statistical probability related formula that describes the rate of the behaviour of rare events. Pr 1 event 0. The Poisson distribution is used to describe the distribution of rare events in a large population.
So can we use binomial and Poisson interchangeably for rare event. 1 Pr1 event over Δt t. To compare the pace of life in different countries investigators measured the speed with which postal clerks completed a simple request.
The binomial distribution model allows us to compute the probability of observing a specified number of successes when the process is repeated a specific number of times eg in a set of patients and the outcome for a given patient is either a success or a failure. Read on for word lists on task-oriented relationship-oriented introverted and extroverted behavior. In the following sections well explain each of these terms one by one.
When describing distributions on the AP Statistics exam there are 4 key concepts that you need to touch on every time. Discrete random variables are usually counts.
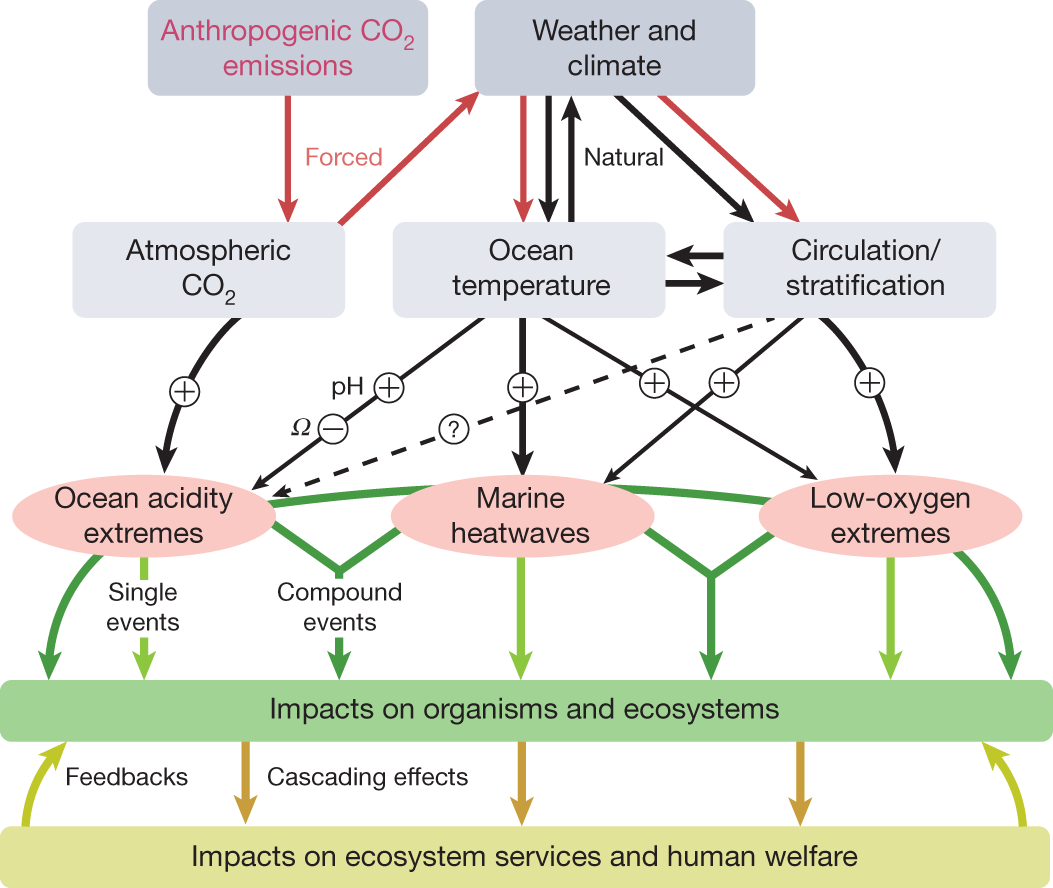
Biogeochemical Extremes And Compound Events In The Ocean Nature

Poisson Distribution An Overview Sciencedirect Topics

The Behavioral Turn In Flood Risk Management Its Assumptions And Potential Implications Kuhlicke 2020 Wires Water Wiley Online Library

0 Comments